Café Discovery: mathematics and science, philosophy and religion

( – promoted by buhdydharma )

Where were we?

(Part I:  250 years of history)

Oh, yes.  Poisson, purportedly the most prolific mathematicians in terms as the number of publications, was a student of LaGrange and La Place at École Polytechnique in Paris.

LaPlace was a student of d’Alembert, but there we lose track of the lineage, since d’Alembert attended one of the colleges in the University Paris…which was decommissioned and dispersed during the French Revolution, so records are lost.  Or because I am not a historian and I am not planning a trip to Paris to search for said records.

LaGrange, on the other hand, was a self-taught mathematician, mostly, whom Leonhard Euler chose to nurture to be his heir as Director of the Prussian Academy of Sciences in Berlin.  Euler even left Berlin for St. Petersburg in 1766, happy to return now that Catherine was on the path to becoming the Great, so that LaGrange could begin his tenure.  For that reason Euler is generally agreed to hold the position of LaGrange’s academic supervisor.

I identify with what LaGrange accomplished by teaching himself mathematics.  While I had some wonderful teachers during my years as a student, the thing that they accomplished the most was to help me learn how to teach myself.    I’ve always tried to remember that in my own teaching.

You’re wondering about the image to the left?  Read on.

Leonard Euler is my mathematical ancestor?  I rock!  Actually, I was more than a little dumbfounded when I discovered that.  Whereas Poisson may have been the most prolific writer on mathematical topics, there may have been no more fertile mind than Euler’s.

This guy has been on Swiss currency and Swiss, German, and Russian stamps. About his influence on mathematics, LaPlace said,

Read Euler, read Euler, he is the master of us all.

A summary of Euler’s accomplishment would taken much more space than I have available.  Keeping it small, he is the inventor of the notation we use today to describe exponential and logarithmic functions, discoverer of the complex numbers and through them the sine and cosine functions.  So, in a sense, he invented trigonometry.  I prefer to think that it already existed and he just discovered it.

One of the thrills of my graduate education was being able to read Euler’s own words (in the original Latin) in a first edition of the book (owned by the University of Oregon) in which he defined the trigonometric functions.

At the top end of mathematics he proved remarkable results in applied mathematics, geometry, graph theory, logic, mathematical physics, and number theory.

He was also a biblical literalist, raised in the Reformed Church.  A Calvinist.  Ack!  And during this time period religion played a vital role in education, for better or worse.

Euler received his Ph.D. in 1726 from the University of Basel.  He was a student of Johann Bernoulli, at the time considered to be the greatest mathematician in Europe.  Euler’s dissertation was on the propagation of sound.  Bernoulli had to convince Euler’s father that Leonhard’s Master of Philosophy degree thesis comparing the philosophies of Descartes and Newton showed he was more suited for mathematics than to become a pastor.

Johann Bernoulli was born into a family of spice traders, except for his older brother Jacob, who was a mathematics professor at Basel.  His father wanted him to become a spice trader as well, but Johann resisted and convinced his father to allow him to study medicine.  Not really being the doctor type, he studied mathematics from Jacob on the side.  Jacob was perhaps the first mathematician to actually teach the calculus of Leibniz.  Johann was his first calculus student.  His major work was in the brand new field of differential equations.

Once upon a time Johann was hired by a Guillaume François Antoine de L’Hôpital to tutor him in mathematics, under a contract that allowed  L’Hôpital to use the knowledge he learned from Bernoulli as he pleased.  L’Hôpital used his notes to publish the first calculus text book.  L’Hôpital’s Rule was discovered by Johann Bernoulli.

Jacob Bernoulli was a student of theology and became a minister, but he also studied mathematics and astronomy.  He also had the good fortune to be a correspondent of Gottfried Leibniz while Leibniz wrote about his conception of calculus.  Jacob founded a school of mathematics and the sciences in the city of Basel prior to being appointed a professor at the university, upon the completion of a dissertation on the solutions of some arithmetic and geometric problems arising from the study of the three-body problem in astronomy.  That’s his gravestone, complete with logarithmic spiral at the bottom, on the right.  It might have proved more appropriate to have used the lemniscate that was named after him.

Gottfried Leibniz???  Godfrey Daniels!  This man developed calculus, independently from Newton.  He was the first to discuss the binary number system as well.  That line of thought, of course, leads to the computer in front of which you are sitting.

Leibniz is considered to have contributed equally to the field of philosophy, where he is most remembered for optimism, i.e.

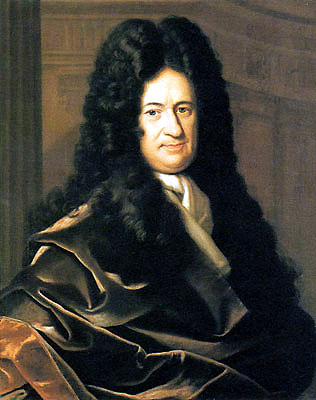
his conclusion that our universe is, in a restricted sense, the best possible one God could have made.

I remember fondly reading, some time in my teens, my older brother’s copy of Voltaire’s Candide, wherein Voltaire mocked the philosophy of optimism ferociously.  My brother, of course, was not using it.  I don’t think he ever did.

Leibniz is ranked with Spinosa and Descartes as the leading rationalists of the 17^th century.

Leibniz’ dissertation and degree were in law in 1666.  But that year he also published his first philosophical text.  And he studied mathematics for a semester under Erhard Weigel at Jena University.  Weigel was widely noted as a teacher and popularizer of science. It is known Weigel received a doctorate in philosophy in 1650 from Leipzig, but his advisor is unknown.

Leibniz became a diplomatic  representative of the Elector of Mainz.  In that job, he encouraged France to invade Eqypt, which didn’t go so well for a guy named Napoleon 126 years later.

But that got him to Paris, where he decided his education in mathematics and physics was substandard, so he became a student of a Dutch guy named Christiaan Huygens.  Huygens taught him how to teach himself mathematics, and the rest, as they say, is history.

Huygens, a friend of Descartes, was himself no slouch in the fields of mathematics, astronomy, and physics.  He argued that light consisted of waves (he was partly right), contributed to Leibniz’ creation of calculus, discovered the moon Titan of Saturn, and made the first known sketch of the Orion Nebula (the interior portion of which is known as the Huygens Region).  He formulated Newton’s second law of motion, which Newton generalized.

The change of momentum of a body is proportional to the impulse impressed on the body, and happens along the straight line on which that impulse is impressed.

Huygens proved this in quadratic form, but did not have the tools of calculus needed to prove the general case.

Encouraged by Blaise Pascal, Huygens published the first book on probability.  In his spare time, he invented the pendulum clock, a balance-spring clock, and a pocket watch.  He also wrote a book about life on other planets named Cosmotheoros – The celestial worlds discover’d: or, conjectures concerning the inhabitants, plants and productions of the worlds in the planets (the link takes you to an English translation, from the Greek).

Huygens had two advisers, one of whom had two advisers, one of whom was also an adviser of René Descartes and the other of whom was also Blaise Pascal’s adviser.

The three amigos?

To be continued